Из металлической проволоки сделаны две одинаковые рамки
Из металлической проволоки сделаны две одинаковые рамки




Из металлической проволоки сделаны две одинаковые рамки. Рамка 1 находится в однородном магнитном поле с индукцией и в начальный момент времени расположена относительно линий магнитной индукции так, как показано на рис. 1. Рамка 2 находится в однородном магнитном поле с индукцией
линии магнитной индукции которого направлены так, как показано на рис. 2.
В момент времени t = 0 рамку 1 начинают вращать (направление вращения указано стрелкой), а модуль индукции B2 начинает изменяться с течением времени t по закону
Установите соответствие между графиками зависимостей физических величин от времени и физическими величинами. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
1) Магнитный поток, пронизывающий рамку 1.
2) Магнитный поток, пронизывающий рамку 2.
3) ЭДС индукции, возникающая в рамке 1.
4) Модуль ЭДС индукции, возникающей в рамке 2.
Согласно закону электромагнитной индукции Фарадея, ЭДС индукции определяется выражением
где — поток магнитного поля.
Для первой рамки где
— угол между нормалью к контуру и вектором индукции магнитного поля,
— площадь контура,
— начальная фаза,
— угловая частота вращения рамки. В начальный момент поток через рамку 1 равен нулю, затем он будет изменяться по закону синуса. Производная магнитного потока, а в свою очередь и ЭДС индукции, будет изменяться по закону косинуса. На графике 1 изображена ЭДС индукции, возникающая в рамке 1. (А — 3)
Вторая рамка расположена перпендикулярно магнитному полю. Магнитный поток изменяется за счет изменения величины индукции магнитного поля, которое меняется линейным образом: Следовательно, на графике 2 изображен магнитный поток, пронизывающий рамку 2. Стоит отметить, что производная магнитного потока по времени в этом случае является постоянной величиной и, следовательно, ЭДС индукции, возникающая во второй рамке, постоянна и не зависит от времени. (Б — 2)
из металлической проволоки сделаны две одинаковые рамки
ВАЖНО! Для того, что бы сохранить статью в закладки, нажмите: CTRL + D
Задать вопрос ВРАЧУ, и получить БЕСПЛАТНЫЙ ОТВЕТ, Вы можете заполнив на НАШЕМ САЙТЕ специальную форму, по этой ссылке >>>
26 июняНовые варианты прошедших ЕГЭ по математике: здесь.
5 июня Наши мобильные приложения могут работать оффлайн.
Андроид iOS
− Examer из Таганрога;
− Учитель Думбадзе В. А.
из школы 162 Кировского района Петербурга.
Наша группа ВКонтакте
Мобильные приложения:
Из металлической проволоки сделаны две одинаковые рамки. Рамка 1 находится в однородном магнитном поле с индукцией и в начальный момент времени расположена относительно линий магнитной индукции так, как показано на рис. 1 . Рамка 2 находится в однородном магнитном поле с индукцией линии магнитной индукции которого направлены так, как показано на рис. 2.
В момент времени t = 0 рамку 1 начинают вращать (направление вращения указано стрелкой), а модуль индукции B2 начинает изменяться с течением времени t по закону
Установите соответствие между графиками зависимостей физических величин от времени и физическими величинами. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
1) Магнитный поток, пронизывающий рамку 1.
2) Магнитный поток, пронизывающий рамку 2.
3) ЭДС индукции, возникающая в рамке 1.
4) Модуль ЭДС индукции, возникающей в рамке 2.
Согласно закону электромагнитной индукции Фарадея, ЭДС индукции определяется выражением
где — поток магнитного поля через замкнутый контур, — угол между нормалью к контуру и вектором индукции магнитного поля, — площадь контура, — начальная фаза, — угловая частота вращения рамки.
В начальный момент времени поток через рамку 1 равен нулю, затем рамка начинает вращаться и поток будет изменяться по закону синуса. Производная магнитного потока, а в свою очередь и ЭДС индукции будет изменяться по закону косинуса. На графике 1 изображена ЭДС индукции, возникающая в рамке 1.
Вторая рамка расположена перпендикулярно магнитному полю. Магнитный поток изменяется за счет изменения величины индукции магнитного поля, которое меняется линейным образом. Следовательно на графике 2 изображен магнитный поток, пронизывающий рамку 2. Стоит отметить, что производная магнитного потока по времени в этом случае является постоянной величиной и, следовательно, ЭДС индукции, возникающая во второй рамке, постоянна и не зависит от времени.
26 июняНовые варианты прошедших ЕГЭ по математике: здесь.
5 июня Наши мобильные приложения могут работать оффлайн.
Андроид iOS
− Examer из Таганрога;
− Учитель Думбадзе В. А.
из школы 162 Кировского района Петербурга.
Наша группа ВКонтакте
Мобильные приложения:
Из металлической проволоки сделаны две одинаковые рамки. Рамка 1 находится в однородном магнитном поле с индукцией и в начальный момент времени расположена относительно линий магнитной индукции так, как показано на рис. 1 . Рамка 2 находится в однородном магнитном поле с индукцией линии магнитной индукции которого направлены так, как показано на рис. 2.
В момент времени t = 0 рамку 1 начинают вращать (направление вращения указано стрелкой), а модуль индукции B2 начинает изменяться с течением времени t по закону
Установите соответствие между графиками зависимостей физических величин от времени и физическими величинами. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
1) Магнитный поток, пронизывающий рамку 1.
2) Магнитный поток, пронизывающий рамку 2.
3) Модуль ЭДС индукции, возникающей в рамке 1.
4) Модуль ЭДС индукции, возникающей в рамке 2.
Согласно закону электромагнитной индукции Фарадея, ЭДС индукции определяется выражением
где — поток магнитного поля через замкнутый контур, — угол между нормалью к контуру и вектором индукции магнитного поля, — площадь контура, — начальная фаза, — угловая частота вращения рамки.
В начальный момент времени поток через рамку 1 равен нулю, затем рамка начинает вращаться и поток будет изменяться по закону синуса. На графике 1 изображен магнитный поток, пронизывающий рамку 1.
Вторая рамка расположена перпендикулярно магнитному полю. Магнитный поток изменяется за счет изменения величины индукции магнитного поля, которое меняется линейным образом. Производная магнитного потока по времени, а в свою очередь и ЭДС индукции в этом случае является постоянной величиной и, следовательно, ЭДС индукции, возникающая во второй рамке, постоянна и не зависит от времени. Следовательно на графике 2 изображен модуль ЭДС индукции, возникающей в рамке 2.
В современных научных и технических устройствах часто используются линейные датчики индукции магнитного поля, работа которых основана на эффекте Холла. Этот эффект состоит в возникновении поперечной разности потенциалов в проводнике или полупроводнике с электрическим током, находящемся в магнитном поле, перпендикулярном току. Пусть вдоль однородного длинного образца полупроводника прямоугольной формы с поперечным сечением размерами b = 0,3 мм и d = 8 мм и концентрацией носителей заряда e положительного знака («дырок»), равной n = 5 ∙ 10 18 см −3 , течёт постоянный ток I = 200 мА, а сам образец находится в однородном магнитном поле с индукцией B = 1,5 Тл, направленной перпендикулярно плоскости образца, вдоль его ребра b (см. рисунок). Чему равна при этом холловская разность потенциалов Ux между гранями образца, параллельными вектору магнитной индукции и току?
1. Когда носитель положительного заряда движется под действием электрического поля вдоль образца полупроводника с «дрейфовой» скоростью v по направлению тока I, на него со стороны магнитного поля, направленного «вверх» перпендикулярно скорости и большой плоскости образца, действует сила Лоренца отклоняющая его вправо по ходу движения (см. рис.).
2. Это отклонение продолжается до тех пор, пока на противоположных малых гранях образца не накопятся заряды, достаточные для создания электрического поля Холла Eх в обратном направлении, компенсирующего воздействие магнитного поля: то есть а разность потенциалов между гранями проводника
3. Сила тока равна потоку зарядов через площадь сечения проводника: где env — заряд, пересекающий единицу площади поперечного сечения проводника за единицу времени. Отсюда
4. Подставляя полученное выражение скорости v в формулу для окончательно получаем:
Расстояние между двумя одинаковыми металлическими шариками намного больше их радиусов. Когда на шарики поместили некоторые заряды, сила отталкивания между ними оказалась равной . После того, как шарики соединили тонкой проволокой, а затем убрали ее, шарики стали отталкиваться с силой . Определить первоначальные заряды шариков и . Электрическая постоянная .
Поскольку по условию задачи шарики достаточно удалены друг от друга, для силы взаимодействия между ними справедлив закон Кулона: . Потенциалы шариков до соединения их проволокой можно определить по формуле для потенциала уединенной заряженной сферы: , , где — радиус каждого из шариков. После соединения шариков проволокой заряды на них перераспределятся так, что потенциалы шариков станут одинаковыми: . Пренебрегая емкостью проволоки, запишем закон сохранения заряда в системе: . Поскольку радиусы шариков равны, из равенства их потенциалов после соединения проволокой следует, что на каждом из шариков будет находиться один и тот же заряд: . В результате этого величина силы взаимодействия примет значение: . Имеем систему уравнений: , . Находя из нее и , получаем ответ: , .
1021. Два провода изготовлены из одного материала и площади их сечений одинаковы. Во сколько раз сопротивление одного провода (длиной 10 м) больше сопротивления другого провода (длиной 1,5 м)?
1022. Каково сопротивление медной струны сечением 0,1 мм2 и длиной 10 м.
1023. Железная и медная проволоки равной длины имеют одинаковые сечения. Одинаково ли сопротивление проволок? Если нет, то какая из них будет иметь большее сопротивление и во сколько раз?
1024. Медный тросик имеет длину 100 м и поперечное сечение 2 мм2? Чему равно его сопротивление?
1025. В электрической цепи общая длина подводящих железных проводов сечением 1 мм2 равна 5 м. Определите сопротивление подводящих проводов.
1026. На рисунке 101 изображены медный, алюминиевый и железный проводники. Вычислите сопротивление каждого проводника.
1027. Медный трамвайный провод имеет длину 3 км и площадь поперечного сечения 30 мм2. Чему равно сопротивление провода?
1028. Имеются две проволоки одинакового сечения и материала. Длина первой 20 см, а второй 1,5 м. Сопротивление какой проволоки больше и во сколько раз? Почему?
1029. Имеются две проволоки одинаковой длины и материала. Сечение одной проволоки 0,2 см2, а другой 4 мм2. Сопротивление какой проволоки больше и во сколько раз? Почему?
1030. Имеются две проволоки одного и того же материала. Длина первой проволоки 5 м, а второй 0,5 м; сечение первой 0,15 см2, а второй 3 мм2. Сопротивление какой проволоки больше и во сколько раз?
1031. Имеются два алюминиевых провода одинаковой длины, но разного сечения. Сечение первого 0,1 см2, а второго 2 мм2. Сопротивление первого 2 Ом. Определите сопротивление второго. (Задачу следует решать, не прибегая к формуле.)
1032. Удельное сопротивление никелина 0,45 мкОм • м. Объясните, что это значит.
1033. Подсчитайте в уме (конечно, не прибегая к формуле), какое сопротивление имеет алюминиевый провод длиной 20 м и сечением 1 мм2.
Сопротивление провода длинной 1 м и сечением 1мм=0.028 Ом ; сопротивление 20 м этого провода будет равно 0.028*20=0.56 Ом.
1034. Подсчитайте в уме сопротивление никелиновой проволоки длиной 1 м и сечением 0,1 мм2.
1035. Какого сечения нужно взять алюминиевую проволоку, чтобы ее сопротивление было такое же, как у медной проволоки сечением 2 мм2, если длины обеих проволок одинаковы?
1036. Рассчитайте по формуле сопротивление километра медного трамвайного провода, если его сечение 0,65 см2.
1037. Длина медных проводов, соединяющих энергоподстанцию с потребителем электроэнергии, равна 2 км. Определите сопротивление проводов, если сечение их равно 50 мм2.
1038. В автомобильном аккумуляторе площадь поверхности пластинок S = 300 см2, расстояние между ними 2 см. Пластинки погружены в 20%-ный раствор серной кислоты с удельным сопротивлением ρ = 0,015 Ом • м. Определите сопротивление слоя кислоты между пластинками.
1039. Телеграфный провод между Москвой и Санкт-Петербургом сделан из железной проволоки диаметром 4 мм. Определите сопротивление провода, если расстояние между городами около 650 км.
1040. Каково сопротивление платиновой нити, радиус сечения которой 0,2 мм, а длина равна 6 см?
1041. Какова длина медной проволоки сечением 0,8 мм2 и сопротивлением 2 Ом?
1042. Четыре провода — медный, алюминиевый, железный и никелиновый — с одинаковым сечением 1 мм2 имеют одинаковое сопротивление 10 Ом. Какова длина каждого провода?
1043. Медная и алюминиевая проволоки имеют одинаковую длину. Какое сечение должно быть у алюминиевой проволоки, чтобы ее сопротивление было таким же, как у медной проволоки с площадью поперечного сечения 2 мм2?
1044. Для реостата, рассчитанного на 20 Ом, используют никелиновую проволоку длиной 100 м. Найдите сечение проволоки.
1045. Железная проволока сопротивлением 2 Ом имеет длину 8 м. Каково ее сечение?
1046. Длина металлической нити электролампочки равна 25 см, удельное электрическое сопротивление материала нити ρ = 0,2 Ом • м. Каково сечение нити, если ее сопротивление в нагретом состоянии равно 200 Ом?
1047. Для реостата, рассчитанного на 20 Ом, нужно взять никелиновую проволоку длиной 5 м. Какого сечения должна быть проволока?
1048. Если вместо никелиновой проволоки в предыдущей задаче взять для реостата железную проволоку такого же размера, то каково будет сопротивление реостата?
1049. Может ли медный провод длиной 100 м с поперечным сечением 4 мм2иметь сопротивление 5 Ом?
1050. Медная спираль, состоящая из 200 витков проволоки сечением 1 мм2, имеет диаметр 5 см. Определите сопротивление спирали.
1051. По никелиновому проводнику длиной 10 м, сечением 0,5 мм2 проходит ток силой 1 А….
1052. Вычислить удельное сопротивление круглого провода, диаметр сечения которого 1 см, если кусок этого провода длиной 2,5 м имеет сопротивление 0,00055 Ом.
1053. Чему равно удельное сопротивление ртути при 0 °С?
1054. Два куска железной проволоки имеют одинаковый вес, а длина одного из этих кусков в 10 раз больше длины другого….
1055. Какой длины потребуется взять константановую проволоку сечением 1 мм2 для изготовления эталона в 2 Ом?
1056. Из манганиновой проволоки изготовлен эталон, который имеет сопротивление 100 Ом при 15 °С. Каково будет сопротивление этого эталона при 5 °С?
1057. Сколько требуется меди на провод длиной 10 км, сопротивление которого должно быть 10 Ом? Плотность меди ρ = 8,5 г/см3.
1058. Для изготовления реостата сопротивлением 2 Ом взяли железную проволоку сечением 3 мм2. Определите массу проволоки.
1059. Никелиновая спираль электроплитки имеет длину 5 м и площадь поперечного сечения 0,1 мм2. Плитку включают в сеть с напряжением 220 В. Какой силы ток будет в спирали в момент включения электроплитки?
1060. Через реостат течет ток силой 2,4 А. Каково напряжение на реостате, если он изготовлен из константа- новой проволоки длиной 20 м и сечением 0,5 мм2?
1061. Каково напряжение на концах железной проволоки длиной 12 см и площадью поперечного сечения 0,04 мм2, если сила тока, текущего через эту проволоку, равна 240 мА?
1062. Для изготовления нагревательного прибора, рассчитанного на напряжение 220 В и силу тока 2 А, необходима никелиновая проволока диаметром 0,5 мм. Какой длины надо взять проволоку?
Задание 26. Кольцо радиуса 10 см из тонкой проволоки с сопротивлением 0,01 Ом находится в однородном магнитном поле, линии индукции которого пересекают плоскость кольца под углом 60°. За какое время в кольце выделится количество теплоты 555 мкДж, если магнитная индукция возрастает со скоростью 0,05 Тл/с? Ответ округлите до целых.
Количество теплоты, выделяемое на кольце, можно определить по закону Джоуля-Ленца:
Модуль напряжения в кольце будет равен модулю изменения магнитного потока, проходящий через кольцо, за единицу времени, то есть
где — площадь кольца (площадь круга); Тл/с – скорость изменения магнитной индукции; — синус угла между линиями магнитной индукции и плоскостью кольца. Подставляя эти величины в формулу времени, получаем:
СПАДИЛО.РУ
Цепи постоянного тока
В задании № 12 ОГЭ по физике необходимо понимание явления постоянного тока, процессов, протекающих в цепях постоянного эл.тока, и знание формул, описывающих такие процессы количественно. Полезные сведения, которые могут потребоваться для решения задания, приведены в разделе теории.
Теория к заданию №12 ОГЭ по физике
Сопротивление цилиндрического проводника
Цилиндрическим считается проводник, имеющий круг в поперечном сечении. Сопротивление такого проводника может быть найдено из уравнения:

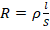
где ρ – удельное эл.сопротивление, индивидуально характерное для различных материалов; l – длина проводника; S – площадь его поперечного сечения.
Последовательное и параллельное соединение проводников
Последовательное соединение:

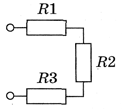
При последовательном соединении сопротивления и напряжения на каждом из резисторов суммируются. Сила тока при этом является неизменной на всех участках разветвления.
Математически это выражается формулами:

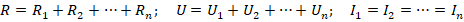
Параллельное соединение:

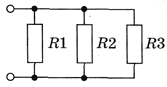
При параллельном соединении суммируются, наоборот, силы тока на каждом из участков. Неизменным при этом остается напряжение. А общее сопротивление определяется по особой формуле.
Математически это выглядит так:

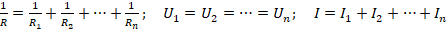
Заряд в проводнике
В проводнике движутся электроны. Эл.ток возникает при их упорядоченном (т.е. направленном) перемещении с какой-то скоростью. Интерес в данном случае представляет величина заряда, который проходит через поперечное сечение данного проводника за определенное время ∆t. Вычислить эту величину можно по формуле:

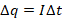
Мощность электрической цепи
Эту величину можно рассчитать по одной из нескольких формул:

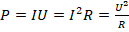
где I – сила тока на исследуемом участке эл.цепи; U – напряжение на этом участке; R – сопротивление.
То или иное уравнение для вычислений следует выбирать в зависимости от известных в условии задачи данных.
Закон Джоуля–Ленца
Когда под воздействием эл.поля в цепи не происходит хим.преобразования вещества и не совершается механическая работа, то работа, производимая эл.полем, ведет только к нагреву проводника. Кол-во теплоты, которое при этом выделяет проводник с эл.током, равно:

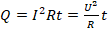
где t – время, в течение которого совершается работа.
Разбор типовых вариантов заданий №12 ОГЭ по физике
Демонстрационный вариант 2018
На рисунке изображена схема электрической цепи, состоящей из трёх резисторов и двух ключей К1 и К2. К точкам А и В приложено постоянное напряжение. Максимальное количество теплоты, выделяемое в цепи за 1 с, может быть получено

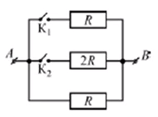
- если замкнут только ключ К1
- если замкнут только ключ К2
- если замкнуты оба ключа
- если оба ключа разомкнуты
Алгоритм решения:
1. Анализируем схему, приведенную в условии. Определяем расчетную формулу.
2–5. Определяем кол-во теплоты в каждой из ситуаций, рассмотренных в утверждениях 1–4. Определяем прав.вариант ответа.
Решение:
- По з-ну Джоуля-Ленца

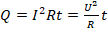 . Поскольку имеет место параллельное соединение разных резисторов, то сила тока в каждой ветке будет различаться. А напряжение при этом во всех ветках одинаково. Поэтому в данном случае удобнее воспользоваться 2-й формулой (в которой присутствует напряжение).
. Поскольку имеет место параллельное соединение разных резисторов, то сила тока в каждой ветке будет различаться. А напряжение при этом во всех ветках одинаково. Поэтому в данном случае удобнее воспользоваться 2-й формулой (в которой присутствует напряжение). - Рассм.утверждение 1. Здесь ток будет протекать по двум параллельным веткам – верхней и нижней. Общее сопротивление при этом равно:

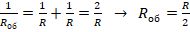 . Тогда за 1 с
. Тогда за 1 с 
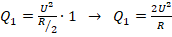 .
. - В утверждении 2 замкнули ключ 2. Следовательно, ток течет по средней и нижней веткам. В этом случае

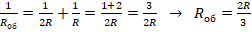 . Искомое кол-во теплоты:
. Искомое кол-во теплоты: 
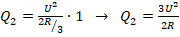 .
. - Если оба ключа замкнуть, то ток потечет по всем 3 веткам. Отсюда:

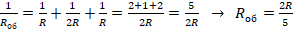 . Кол-во теплоты за 1 с в таком случае составит:
. Кол-во теплоты за 1 с в таком случае составит: 
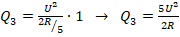 .
. - В утверждении 4 рассмотрен вариант, когда оба ключа разомкнуты. Это означает, что ток течет только по нижней ветке и

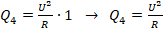 .
. - Сравним полученные кол-ва теплоты. Сравнивать будем с Q4, поскольку полученная для этой величины формула не содержит коэффициента. Итак:

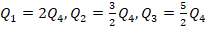 . Отсюда видно, что, во-первых, каждое из Q1–Q3 больше, чем Q4, а во-вторых, среди этих трех значений самое большое имеет Q3. Т.е. максимальное кол-во теплоты выделится, если замкнуть оба ключа.
. Отсюда видно, что, во-первых, каждое из Q1–Q3 больше, чем Q4, а во-вторых, среди этих трех значений самое большое имеет Q3. Т.е. максимальное кол-во теплоты выделится, если замкнуть оба ключа.
Первый вариант (Камзеева, № 3)
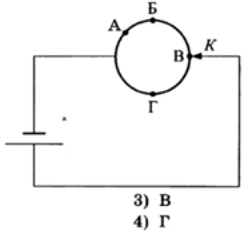
Из однородной металлической проволоки сделано кольцо. Напряжение на полюсах источника тока постоянно. При каком подключении контакта К потребляемая мощность цепи будет минимальной?

Алгоритм решения:
- Записываем формулу для расчета мощности через напряжение и сопротивление. Определяем условие, при котором она будет минимальной.
- Находим зависимость сопротивления от длин проводников.
- Анализируем особенность параллельного соединения проводников и, исходя из этого и выводов п.2, определяем точку подключения ключа.
Решение:
- По условию напряжение на источнике тока является постоянной величиной. Поэтому для расчета мощности удобнее всего воспользоваться такой формулой:

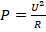 . Из этой формулы следует, что минимальная мощность будет в точке, в которой максимально сопротивление.
. Из этой формулы следует, что минимальная мощность будет в точке, в которой максимально сопротивление. - Сопротивление цилиндрического проводника вычисляется по формуле:

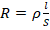 . Поскольку проволока однородна, то ρ в данном случае есть величина постоянная. Постоянна и S, т.к. длина кольца не меняется. Поэтому сопротивление здесь пропорционально длине проводника l. Тогда имеем зависимость: чем больше длина проводника, тем больше сопротивление.
. Поскольку проволока однородна, то ρ в данном случае есть величина постоянная. Постоянна и S, т.к. длина кольца не меняется. Поэтому сопротивление здесь пропорционально длине проводника l. Тогда имеем зависимость: чем больше длина проводника, тем больше сопротивление. - Из схемы цепи видно, что в любом случае соединение проводников будет параллельным. А потому тут следует помнить еще один момент: при параллельном соединении проводников общее сопротивление всегда будет меньше самого меньшего из сопротивлений (что можно проверить опытным путем). Самое маленькое сопротивление у проводника А, т.к. у него наименьшая длина (см.п.2). Поэтому в данном случае ключ нужно подключить в точку, которая является самой удаленной от А. Ею является т.В. Именно так получим максимальное сопротивление и, соответственно (см.п.1), минимальную мощность цепи.
Второй вариант (Камзеева, № 5)
На рисунке показано подключение в сеть постоянного напряжения трех одинаковых ламп.

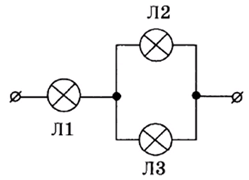
С минимальным накалом будет(-ут) гореть лампа(-ы)
Алгоритм решения:
- Записываем формулу для расчета эл.мощности ламп через силу тока и сопротивление.
- Анализируем приведенную в условии схему и определяем зависимость мощности от силы тока и сопротивления.
- Определяем мощность каждой из ламп, сравниваем их.
Решение:
- Степень накала ламп зависит от величины тепловой мощности, выделяемой на каждой из них. Для определения электрической мощности используем формулу

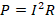 .
. - Сопротивления у ламп равны между собой, т.к. лампы одинаковы. А сила токов будет различаться на участке Л1 и на участке параллельного соединения ламп Л2 и Л3. При параллельном соединении ток делится, причем, поскольку лампы одинаковы, то ток разделится поровну. Т.е. если принять, что через Л1 идет ток I, то через Л2 и Л3 – токи, равные I/2.
- Мощность лампы Л1 будет равной

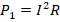 , мощности Л2 и Л3 –
, мощности Л2 и Л3 – 
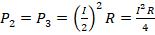 . Из этих формул видно, что мощность ламп Л2 и Л3 в 4 раза меньше, чем Л1. Этой ситуации соответствует ответ №4.
. Из этих формул видно, что мощность ламп Л2 и Л3 в 4 раза меньше, чем Л1. Этой ситуации соответствует ответ №4.
Третий вариант (Камзеева, № 10)
Четыре резистора изготовлены из различных материалов и имеют различные размеры (см. рис.).

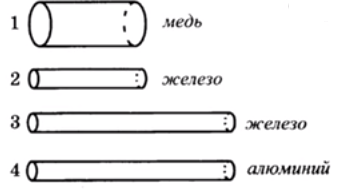
Наибольшее электрическое сопротивление имеет резистор
Источники:
http://phys-ege.sdamgia.ru/problem?id=10323
http://spadilo.ru/zadanie-12-oge-po-fizike/